Hexadezimale Zahlen in der (Web-IO) Praxis

In allen Kulturkreisen wird heute mit dezimalen Zahlen gerechnet. Mit den Ziffern 0..9 gibt es in diesem System für jede Stelle einer Zahl 10 Möglichkeiten. Den Umgang mit diesem System sind die Menschen gewohnt und jeder weiß, dass nach der Zahl 9 die Einerstelle wieder bei Null anfängt und die Zahl 10 mit einer zusätzlichen Zehnerstelle folgt.

In der Computertechnik arbeitet man mit Bits und Bytes, also mit Speicherstellen die jeweils nur den Zustand gesetzt also 1 oder nicht gesetzt also 0 kennt. Das entspricht dem dualen- oder auch binären Zahlensystem. Auch die Web-IO Digital Geräte verarbeiten die Zustände der Inputs und Outputs intern als duale Zahlen.

Duale Zahlen sind für den Menschen leider sehr unübersichtlich. Wer erkennt schon auf Anhieb, dass dual 110001110101 = dezimal 3189 ergibt? Da man jeden Input bzw. Output des Web-IO als eine Stelle einer 12-stelligen Binärzahl sehen muss, macht es Sinn, sich noch einmal mit dieser Materie zu beschäftigen.

Das Umrechnen von Dual- in Dezimal-Zahlen ist nicht schwierig. Dennoch fehlt die spontane Zuordnung zwischen gesetzten Outputs und dem Dezimalwert. Deshalb werden dort, wo der Mensch mit Bits und Bytes jonglieren muss, hexadezimale Zahlen verwendet.

Bei hexadezimalen Zahlen kann die Wertigkeit jeder Stelle durch 15 verschiedene Ziffern dargestellt werden. Da unser dezimales Zahlensystem nur Ziffern von 0 ... 9 kennt, wurde das heaxdezimale System um die Buchstaben A ... F erweitert.

A =10, B=11, C=12, D=13, E=14, F=15.

Hier noch mal etwas übersichtlicher:

Auf den ersten Blick macht die Benutzung des hexadezimalen Zahlensystems die Darstellung der Inputs und Outputs nicht einfacher. Aber schauen wir einmal genau hin. Jede Stelle der hexadezimalen Zahl ist eine Potenz zur Basis 16 multipliziert mit der Ziffer. 16 wiederum ist die 4. Potenz von 2, also 2^4.

Jede Stelle des hexadezimalen Zahlensystems lässt sich deshalb durch Addition der 2er Potenzen 2^0 bis 2^3 errechnen.

Zerlegt man nun eine Dualzahl mit der niedrigsten Stelle beginnend in Vierbit-Bereiche, kann man mit wenig Aufwand zwischen Dualzahlen und hexadezimalen Zahlen umrechnen.

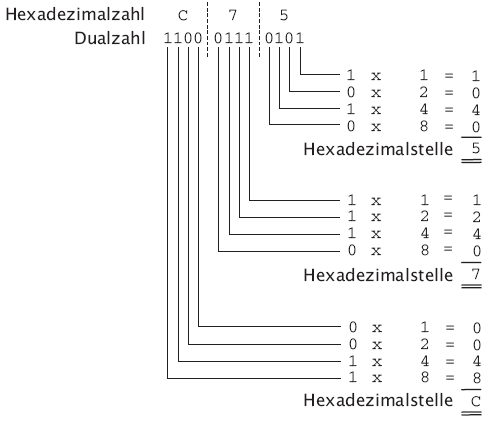
Mit etwas Übung lässt sich das bequem im Kopf rechnen.