Numeri esadecimali nella pratica (Web-IO)

In tutti i circoli culturali si calcola oggi con numeri decimali. Con le cifre 0 - 9 sono disponibili in questo sistema per ogni cifra di un numero 10 possibilità. Le persone sono abituate all’utilizzo di questo sistema e chiunque sa che dopo il numero 9 l’unità ricomincia con zero e che si aggiunge la decina.

Nella tecnologia informatica si lavora con bit e byte, ossia con posizioni di memoria, ciascuna delle quali conosce solo lo stato occupato ossia 1 oppure lo stato non occupato ossia 0. Ciò corrisponde al sistema numerico duale o anche binario. Anche gli apparecchi Web-IO digitali elaborano gli stati degli input e degli output internamente come numeri duali.

I numeri duali purtroppo non sono affatto molto chiari per l’uomo. Chi riconosce di primo acchito che il duale 110001110101 = al decimale 3189? Poiché ogni input od output del Web-IO deve essere visto come il posto di un numero binario a 12 cifre, ha senso occuparci di nuovo di questa materia.

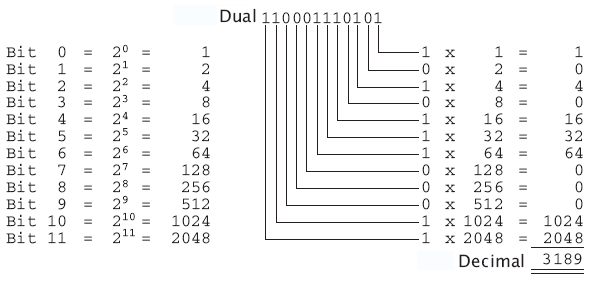
La conversione di numeri duali in numeri decimali non è difficile. Tuttavia manca l’assegnazione spontanea tra gli output impostati e il valore decimale. Pertanto laddove l’uomo deve destreggiarsi con bit e byte vengono utilizzati numeri esadecimali.

Nei numeri esadecimali il valore di ogni posizione può essere rappresentato da 15 diverse cifre. Poiché il nostro sistema numerico decimale conosce solo cifre da 0 a 9, il sistema esadecimale è stato ampliato con le lettere dalla A alla F.

A =10, B=11, C=12, D=13, E=14, F=15.

Ecco di nuovo in modo un po’ più chiaro:

Al primo sguardo l’utilizzo del sistema numerico esadecimale non semplifica la rappresentazione degli input e degli output. Ma guardiamo in modo più preciso. Ogni posizione del numero esadecimale è una potenza a base 16 moltiplicata per la cifra. 16 è d’altronde la quarta potenza di 2, ossia 2^4.

Ogni posizione del sistema numerico esadecimale può essere pertanto calcolata aggiungendo la seconda potenza da 2^0 a 2^3.

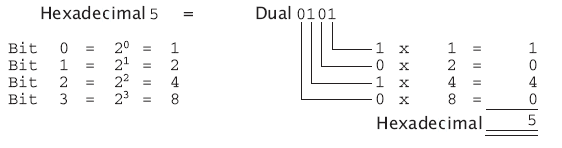
Se ora si scompone un numero duale con la posizione inferiore iniziando in range di quattro bit, si possono convertire facilmente i numeri duali e i numeri esadecimali.

Con un po’ di esercizio si può calcolare comodamente a mente.