Hexadecimal numbers with the Web-IO

All cultures today calculate using decimal numbers. In the decimal system there are 10 possibilities for each place in a number. People are accustomed to using this system, and everyone knows that after the number 9 the ones place starts over at zero and the number 10 follows with an additional tens place.

In computer technology we use bits and bytes, i.e. with storage positions where the state is either set i.e. 1 or not set i.e. 0. This corresponds to the dual or binary numbering system. Web-IO Digital devices also process the states of the inputs and outputs internally as binary numbers.

Binary numbers are difficult for people to comprehend. Who can tell you off the top of their head that binary 110001110101 equals decimal 3189? Since you have to look at each input and output on the Web-IO as a place in a 12-digit binary number, it makes sense to review this material again.

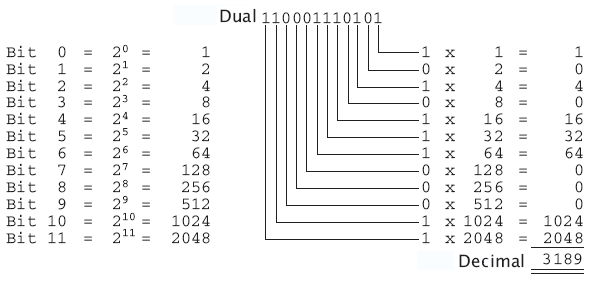
Converting from binary to decimal numbers is not difficult. Nevertheless, there is no immediately apparent association between the set outputs and the decimal value. This is why hexadecimal numbers are used where people have to juggle bits and bytes.

In hexadecimal the value of each place can be represented by 15 different numbers. Since our decimal numbering system only includes numbers from 0 ... 9, the hexadecimal system was expanded by adding the letters A ... F.

A =10, B=11, C=12, D=13, E=14, F=15.

Here is a clearer explanation:

At first glance use of the hexadecimal number system does not seem to make representation of the inputs and outputs any simpler. But let’s take a closer look. Each place in a hexadecimal number is a power of 16 times the digit. 16 in turn is the 4th power of 2, or 2^4.

Each place in the hexadecimal number system can therefore be calculated by adding the 2nd powers 2^0 to 2^3.

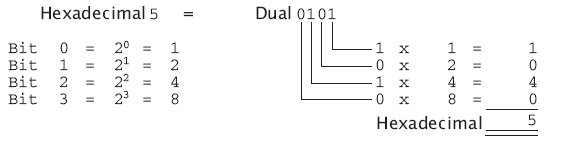
If you now break down a binary number into four-bit ranges beginning with the lowest place, you can easily convert between binary numbers and hexadecimal numbers.

With a little practice this is even easy to do in your head.